根據定義：

B樹，是一種自平衡的搜尋樹，能夠保持數據有序。這種資料結構能夠讓查找數據、順序訪問、插入數據及刪除的動作，都在對數時間內完成。B樹，概括來說是一個一般化的二元搜尋樹（binary search tree）一個節點可以擁有2個以上的子節點。與自平衡二元搜尋樹不同，B樹適用於讀寫相對大的數據塊的存儲系統，例如磁碟。B樹減少定位記錄時所經歷的中間過程，從而加快存取速度。B樹這種資料結構可以用來描述外部存儲。這種資料結構常被應用在資料庫和文件系統的實現上。
-- Wikipedia B樹

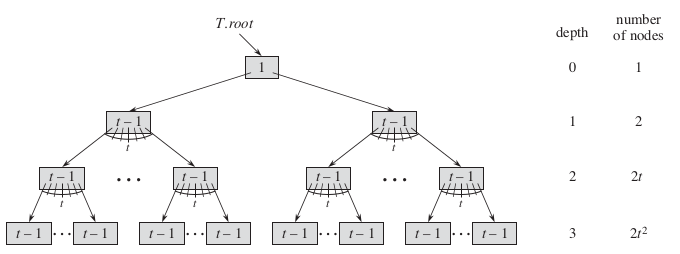
由於 B-tree 將更多的 key/pointer 結合成一個節點中，透過這樣平坦的樹，使得原本很耗時的搜索減少。

B-Tree Create

B-TREE-CREATE (T)
    x = ALLOCATE-NODE()
    x.leaf = TRUE
    x.n = 0
    DISK-WRITE(x)
    T.root = x

B-Tree Search

B-TREE-SEARCH (x, k)
    i = 1
    while i <= x.n and k > x.key[i]
        i = i + 1
    if i <= x.n and k == x.key[i]
        return (x, i)
    elseif x.leaf
        return NIL
    else DISK-READ(x.c[i])
        return B-TREE-SEARCH(x.c[i], k)

B-Tree Split Child

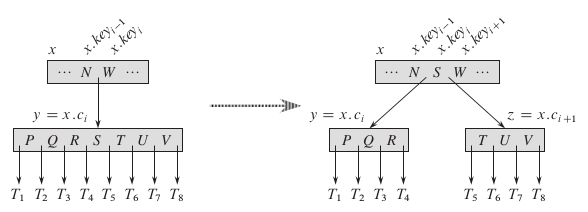
B-TREE-SPLIT-CHILD (x, i)
    z = ALLOCATE-NODE()
    y = x.c[i]
    z.leaf = y.leaf
    z.n = t - 1
    for j = 1 to t - 1
        z.key[j] = y.key[j+t]
    if not y.leaf
        for j = 1 to t
            z.c[j] = y.c[j+1]
    y.n = t - 1
    for j = x.n + 1 downto i + 1
        x.c[j+1] = x.c[j]
    x.c[i+1] = z 
    for j = x.n downto i
        x.key[j+1] = x.key[j]
    x.key[i] = y.key[t]
    x.n = x.n + 1
    DISK-WRITE(y)
    DISK-WRITE(z)
    DISK-WRITE(x)